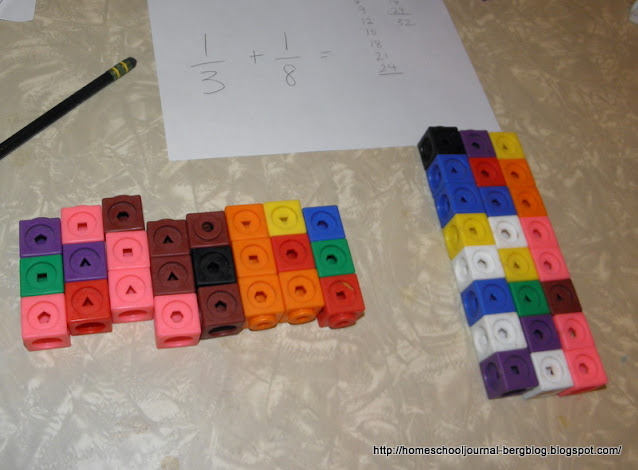Form II: Arithmetic: Fractions (3-6)
Fractions are pretty easy on the most basic level because we often use fractional terms when we talk about sharing things or dividing things. It is not always easy for then to make the leap to more abstract concepts, however. I start their understanding of fractional values with concrete manipulatives such as the geoboard and math blocks.
Understanding Fractional Values
Understanding Fractional Values Using a Geoboard
First I establish a baseline that one square on the geoboard has the value of one unit. I let them make areas of two or three or more if they wish. Through practice, they can see that the squares do not have to be touching to count as units. Then I give them the triangle above and ask them what value it has. If they cannot see that it is 1/2, then I move the square so that it is on top of the triangle and usually they can see that it is 1/2 of the square. If they cannot, I take a square piece of paper and fold it into two equal triangles and tear it apart, so they can see that the triangle is one part of two parts. I show them how the numbers in the fraction work to show these two concepts.
First I establish a baseline that one square on the geoboard has the value of one unit. I let them make areas of two or three or more if they wish. Through practice, they can see that the squares do not have to be touching to count as units. Then I give them the triangle above and ask them what value it has. If they cannot see that it is 1/2, then I move the square so that it is on top of the triangle and usually they can see that it is 1/2 of the square. If they cannot, I take a square piece of paper and fold it into two equal triangles and tear it apart, so they can see that the triangle is one part of two parts. I show them how the numbers in the fraction work to show these two concepts.
We then play around with making two half-units or three half-units to also show that the half-units do not have to be touching to count as half-units.
I then present to them this triangle as ask if they can tell what is the area of this triangle.If they cannot tell, I do the same as I did with the one unit square, and put a two unit square over the triangle. They then can recognize the two units and leap to the conclusion that the triangle, being half, is one unit in area. If the student still has trouble understanding this, you can cut a triangle that is the same size as the triangle on the board that is in question. Cut off the top of the paper triangle and turn it around to fit next to the bottom half to form a square the same size as the one unit square on the board.
Once they understand how to manipulate the areas by making whole units and dividing them in half, more complex figures can be made such as triangles that are not right triangles.
Have them make rectangles or squares out of paper and cut them if they need to, but usually by this time, they can easily use the geoboard to figure out the areas.
Understanding Fractional Values Using Blocks

We then go on to finding halves on math blocks. These blocks are from Math-U-See, but Cuisenaire rods would work even better because they are not pre-marked with units. I have them take a block and find two blocks of the same color that can form a train that equals the chosen block. For example, if the chosen block is this purple block, they need to choose two blocks of the same color that equal its length, in this case, two pink ones.
I have them find all the halves with the blocks and record them on graph paper. I want to make sure they understand that one-half is a relationship rather than a fixed quantity. This is not usually too hard of a concept because they are used to seeing that one whole apple is smaller than one-half of a pie, for example. It is important to set this as a foundation, however, before we go on to more abstract concepts and begin manipulating the fractions with operations.
Equivalent Fractions
Equivalent Fractions Using Blocks
A few days after our first exploration with blocks, we again use blocks, this time finding all the equivalent fractions. He finds all the equivalent one color trains for the 10, 8 and 6 blocks. We go over the fact that the light blue blocks are 1/2 of the dark blue blocks and the orange blocks are 1/5 of the dark blue blocks and so on. This is also showing relational values as before, but is also introducing the concept of equivalent fractions.
I can now give him addition and subtraction problems with like denominators. I usually like to give these first as word problems because they are easier to visualize. You can say something like, "We have seven members in our family. Two are wearing red shirts today and three are wearing white. Altogether, how many people are wearing either red or white shirts?" After a few of these, you can begin just putting down the problems and have him come up with possible word problems to go with them. You can check comprehension by seeing if he can come up with the appropriate problems to go with the numbers. Soon he should begin making up his own number and word problems and this can be quite fun even for the more creative, less-math oriented students.
Equivalent Fractions Using Paper Folding
Now, it is time to do some more work on equivalent fractions. I use a plain piece of paper and fold it in half. I open it back up again and ask what fraction of the whole piece of paper would one of the two pieces be? He can answer either 1 over 2 or 1-half. I write that down on a separate piece of paper a couple inches down the page. Then I ask what would the whole piece be called if you included both halves. You are looking for two over two, but if he doesn't understand you can ask what if I put the two halves together, then how many halves would you have? Write it 2/2 on the top of the page. Fold the page in half again, and add the fractions, 4/4, 2/4. and a new row for 1/4 as he answers your inquiries of how many total squares are there, how many is on half the page and how many is one section of the whole. Continue in this manner, as you continue to fold the paper.
You can then work a problem or two using unlike fractions and helping him as he needs to look through the list you have just made for equivalent fractions.
At another time, you can fold a piece of paper into thirds first before beginning to fold in halves, making lists of equivalent fractions as you go.
Next, we use sticks of Unifix cubes to generate a greater variety of equivalent fractions than was possible with paper folding.
First we began with a stick of eight cubes and I guided him through finding equivalent fractions by asking questions such as,
What fraction of the whole stick is one cube?
Can you break your stick into four equal parts? If the stick you started with was one whole stick, what fraction of it would one of your parts be?
I continue asking him to break the whole stick into various divisions and asking him what equivalent fractions they are. I record them for him on a sheet of paper as he answers the questions or makes discoveries himself.
Once he seems confident in finding equivalent fractions in this way, I let him decide what stick length he wants to work with.
To assist him, I continue being his scribe for awhile. I divided a couple of sheets of paper into sections, labeling the top of each section with a number. This number is the length of the cube stick. I just record what he tells me. We work on this for as little or as long as he wants. When we continue it on another day, if I feel he is ready, I will let him record his own discoveries to finish his chart of equivalent fractions."Some (students) will see patterns that permit them to abandon the materials quickly; others will alternate between concrete objects and abstract reasoning, or rely solely on physical aids. Each method is equally valid and each should be equally valued."
-Mathematics...A Way of Thinking, Robert Baratta-Lorton
Start With-Go By or Introduction to Addition and Subtraction of Fractions
Then I gave him the problem 1/3 + 1/8 = and told him that with the lists he generated, we could solve this problem.
I asked him to take the first number given on the both list, which in this case was 24, and make two cube sticks of that length. Now break the first cube stick into sticks of 3 in length so that we could change the 1/5 into an equivalent fraction. He made eight sticks. We wrote down the equivalent fraction as 8/24 or eight sticks of three out of a 24 stick cube. The second stick was broken into sticks eight cubes long. We could then write the equivalent fraction for 1/8 as 3/24 or 3 cube sticks 8 cubes long out of a 24 cube stick.
Now solving the problem was easy. We added one cube stick from each group and together and got the answer of 11/24.
He happily did several problems like this.
Multiplication of Fractions on the Geoboard
Beginning with concepts we have already done, we reviewed multiplication on the geoboard.
Then we applied the same concept that we used with the Unifix cube sticks to the geoboard squares. If the big square (rectangle) is one, what fraction of it is the smallest square (rectangle)?
If he has trouble answering this, walk him through it by first asking what the total area of the rectangle is.
In this case, it would be eight, so the smaller rectangle would be two out of the eight or 2/8 of the total area. This process is repeated for several squares, with the student making squares with the value of one and deciding what the fractional value of a smaller square in it.
Once he becomes comfortable finding these fractional values, then we go on to examine the sides of a rectangle on the geoboard. If we say the width is the shortest side and the length is the longest, what fraction of the whole width would one square be? In the above example, it would be one out of three or 1/3. One square of the length would be one out of two or 1/2.
So, what then would two squares be? On the length side, the smaller rectangle is 2/4 and on the width side, the smaller rectangle is 1/2. The area of the smaller rectangle to the larger rectangle is 2/8,
or 2/4 x 1/2 = 2/8.
Once he understands this concept, he can begin recording the fractional values of one square in columns - the length in one column, the width in another and the total area in the third. If he writes it in this way, he should begin to see that the length multiplied by the width equals the area, just as it did for multiplying with whole numbers on the geoboard. He can discover the rules to predict the answers by testing as he works with the problems and seeks out the patterns.