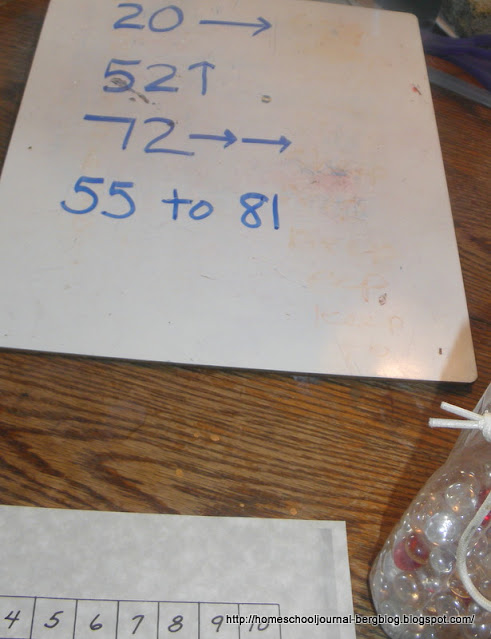Patterns on Number Tables
"Patterns from the core of mathematics. The search for and discovery of these patterns are the foundations of mathematic learning. Each mathematical exploration is undertaken with the assumption that within lies a pattern waiting to be discovered. The search may not always be successful, but it is always to be conducted."- Mathematics...A Way of Thinking, Robert Baratta-Lorton
One day I began our math lesson with a blank 10 x 10 block graph paper with large blocks. I wrote down some of the numbers in the squares. Then I posed the question, "Can you tell me some other numbers to write in the other squares? The numbers I have written already are part of a pattern. If you see my pattern, you will be able write what numbers are missing.
The second day, I supplied a new graph paper sheet but filled out the numbers a little differently. This time I didn't let him write it down, but asked him to tell me where to put the numerals.
The next day, we took a chart and looked at the patterns in it.
What happens to the numbers as they go from left to right in the top row?
What happens to the numbers if we go from right to left across the top row?
Look at the numbers from top to bottom. Can you see any number patterns?
Sometimes we drew lines to clarify what we were saying. A diagonal line can show "doubles."
With that foundation, we then played a game called "Arrow Math." I used a chart that I had filled in myself.
"The rule to my game is that when I write something like this 20 with an arrow behind it, what I mean is 21."
I gave a few more examples until he could give me the answer that followed my rule.
"How about 52 with the arrow pointing up?"
Once he could figure out what one arrow meant, then we tried problems that use more that one arrow at a time. When he tired of this, I posed a different problem.
"What do you think 72 with one arrow pointing right and one arrow pointing up could mean?
Then I posed questions such as, "How can you get from 55 to 81 using the fewest arrows?"
Now he was ready to create problems for me or others to solve.
Then we thought up games to play another day. "What if we pick two numbers that you could get from the first to the second number using only two arrows. Or three...or more, up to 5."
"Or we could use other number tables..."
"One of our goals is to help students refine their language and improve their ability to say what they want to say. If their instructions are unclear and we follow those instructions literally, our students can discover that what they meant may not have been what they said."
- Mathematics...A Way of Thinking, Robert Baratta-Lorton
The next day, we took a chart and looked at the patterns in it.
What happens to the numbers as they go from left to right in the top row?
What happens to the numbers if we go from right to left across the top row?
Look at the numbers from top to bottom. Can you see any number patterns?
Sometimes we drew lines to clarify what we were saying. A diagonal line can show "doubles."
"No preconceived notions should be held as to what students must see. They are not supposed to see anything in particular, only to look. Students cannot be expected to recognize a pattern every time they look. But they will see many more patterns if they look for them than if they do not."- Mathematics...A Way of Thinking, Robert Baratta-Lorton
With that foundation, we then played a game called "Arrow Math." I used a chart that I had filled in myself.
"The rule to my game is that when I write something like this 20 with an arrow behind it, what I mean is 21."
I gave a few more examples until he could give me the answer that followed my rule.
"How about 52 with the arrow pointing up?"
Once he could figure out what one arrow meant, then we tried problems that use more that one arrow at a time. When he tired of this, I posed a different problem.
Then I posed questions such as, "How can you get from 55 to 81 using the fewest arrows?"
Now he was ready to create problems for me or others to solve.
Then we thought up games to play another day. "What if we pick two numbers that you could get from the first to the second number using only two arrows. Or three...or more, up to 5."
"Or we could use other number tables..."